GROUPS,
RINGS, FIELDS AND INTEGRAL DOMAINS
THE ASSUMED OPERATION FOR Z (THE SET OF INTEGERS) IS ADDITION. I AM ONLY PROVIDING THE TABLES FOR MULTIPLICATION for Zn.
DISCUSSION
QUESTION: WHAT IS A RING?
ANALYSIS: RING
RING: (properties)
Addition properties
1-5 AN ABELIAN GROUP
1. Associative property of addition
2. commutative property of addition
3. identity property of addition
4. inverse property of addition
5. distributive property
Multiplication properties
ASSOCIATIVE RING 1-6
6. associative of multiplication (non associative rings also exist: octonions, Sloane's,
A037292, )
OPTIONAL CONDITIONS FOR RINGS:
COMMUTATIVE RING: 1-7
7. commutative of multiplication
(non-commutative rings: Real-valued
 matrices
matrices,
quaternions)
RING WITH AN IDENTITY: 1-8 APPLY
8. multiplicative identity ( Some authors required 8 for it to be a ring)
(with no multiplicative identity: Even-valued
integers, ) There might be an identity for multiplication but sometimes there is none but if it exists it must be unique. Z6 is a commutative ring with an identity. in Z6 only 1 and 5 have multiplicative inverses. These two elements form form the group of units of Z6. Z6 is a typical ring.
RING WITH INVERSES 1-9 BECOMES A FIELD
9. multiplicative inverses (the integers Z have no multiplicative inverses) might not exist but if they do, they must be unique
SYNTHESIS: RING
For a ring is enough to be an Abelian group 1-5. 6 is the associative property of multiplication. Thus 1-6 will make it into an associative ring. 1-5 will make it into a non-associative ring. 7 will make it into a commutative ring. 8 will make it a ring with multiplicative identity, be this ring associative, non-associative, commutative or non commutative. 9 will make it a ring with multiplicative inverses. In the case 1-8 applies and ab = ba = 0 only if a = 0 or b = 0 will make it into an integral domain. An integral domain has no zero divisor; that is, if ab=ba=0 for a ≠ 0 and b ≠ 0. Finally in a ring -ab=a(-b)=-ab and also 0a = a0 =0 these two properties work as a result of 5. You can use 5 to prove both properties.
Z is a ring without multiplicative inverses. Most elements in most rings do not have inverses.
QUESTION: WHAT IS A FIELD?
FIELD:
1-9 must satisfied.
Q is a field. R is a field. C is a field. Zn is a field for n = prime. Zn is a commutative ring with identity. When n is composite Zn has zero divisors, and thus is not even an integral domain.
QUESTION: WHAT IS A SKEW FIELD?
ANALYSIS: SKEW FIELD
if 7 does not apply it is called a SKEW FIELD
SYNTHESIS: SKEW FIELD
A Skew field is therefore a field whose element are does not commute under multiplication.
QUESTION: WHAT IS AN INTEGRAL DOMAIN?
ANALYSIS:
An integral domain is a commutative ring 1-7 with an identity 1-8 in which ab=0 iff a = 0 or b = 0. An integral domain has no zero divisors, that is if ab=ba=0 iff a ≠ 0 and b ≠ 0. Z is an integral domain. Z is commutative. Z has an identity. Z has no inverses. Z has no zero divisors.
SYNTHESIS:
The set of integers is an integral domain. The set of integers is a commutative ring. It has an identity 1. The elements in the set has no inverses and no zero divisors.
INTEGRAL DOMAIN:
2Z has no zero divisors, but it is not an integral domain because it lacks an identity
GROUP:
A UNIT:
AN INVERSE:
A ZERO DIVISOR:
IDENTITY:
PRIME:
COMPOSITE:
EXAMPLES OF RING:
The Natural Numbers is not even a ring because addition does not have inverses.
Z, Q, R, and C are all commutative rings. They all have multiplicative identities. They are all integral domains. Q,R and C are fields. These are but a few of many fields.
ANALYSIS AND SYNTHESIS: MODULAR MATHEMATICS (CLOCK ARITHMETIC)
QUESTIONS: WHAT IS AN IDEMPOTENT? WHAT IS A NILPOTENT?

ORDINARY MULTIPLICATION TABLE:
THE SET OF Z (INTEGERS) FORM A FIELD
IT IS A COMMUTATIVE RING WITH IDENTITY 1
(INTEGER MODULO 0?)
THERE ARE NO ZERO DIVISORS. IN FACT, THE SET OF INTEGERS IS AN
INTEGRAL DOMAIN, AS IT HAS NO ZERO DIVISORS. This integral domain is a ring only and not a field for in this system division is impossible. This is an example of ring that is not a field.
In integer modulo 0, the divisor is 0 itself. This means we would have to
divide by zero to find out answers. However, division by zero is not allowed in ordinary arithmetic. Thus, I am let to conclude I must divide by 1. Dividing by 1 let me to the desired multiplication. For example, 5•5 = 25 and 25 divided by 1 is 25 and this seems to work whenever I multiply any non-negative integer by any other non-negative integer including multiplication by zero. I notice that there is only one idempotent in this system. that is one number satisfying the equation x•x = x, namely 1•1 = 1. Any other observation at this point will have to wait until I can synthesize any further analysis. I must mention that the rational numbers is a field because division is possible there and the integers is only a ring as division does not exists withing the set of integers. This is the reason why the integers does not form a field under multiplication.

INTEGER MODULO 1: (1 is neither prime nor composite)
THERE ARE NO ZERO DIVISORS.
THIS IS NOT AN INTEGRAL: There is no identity 1 ≠ 0 ;1•a = a = a•1
ACTUALLY THE IDENTITY HERE IS 0 AS 0•0 = 0 =0• 0 BUT THIS IS ONLY AN EXCEPTION, ALL OTHER UNITS ARE EQUAL TO 1.
0 ALSO BEHAVES AS A UNIT, BUT THIS IS ALSO AN EXCEPTION
THIS IS THE TRIVIA RING R= 0.
How interesting can be a clock with only one number? The number zero.
Here we could only multiply 0•0 to get 0 and nothing more. According to the rule of
idempotent elements we have x•x = x or as I noted above 0 • 0 = 0. Also x exp n = 0 for some n > 0 in this case n=2 we get that 0 is also a
nilpotent. There are no nonzero
zero divisors. That is, for any a and b in the system ab = 0 for some a ≠ 0 and some b ≠ 0.
We will see the appearance of zero divisor in integer modulo 4 where 2•2 = 0, since 2•2 is 4 in regular multiplication but when dividing 4 by 4 we get 1 remainder 0; thus making (4 = 0 modulo 4) in the sense of explaining the meaning of clock arithmetic.
In integer modulo 1 we are supposed to divide by 1 after multiplying. Example 0•0 =0 and 0÷1 is zero (see ordinary multiplication above with 1 as a divisor only that in ordinary multiplication the elements in the set are infinite.) Also notice that 1 is neither a prime nor a composite number. the following integer modulo is a prime number. Integer modulo with prime numbers give rise to fields. I will explain this later.

INTEGER MODULO 2 ( 2 is a prime number)
THIS IS A FIELD: A COMMUTATIVE RING WITH AN IDENTITY
THERE ARE NO ZERO DIVISORS; this is an integral domain
1 HAS AN INVERSE AS 1•1=1= 1•1; ab = 1 = ba.
THE SET OF UNITS {1} IS THE SET OF NONZERO ELEMENTS THAT HAS A INVERSE
1 IS THE IDENTITY as 1•a = a = a•1
We still have no
zero divisors. Two is a prime number. 1 and 0 are both
idempotent. 0 is the only
nilpotent. Notice there is no need to divide in this modulo by two as the product 1•1 = 1. In the following modulo we will use the concept of division as 2 • 2 is 4. Thus we will say 4 ÷ 3 = 1 or say 4 = 1 (mod 3).
INTEGER MODULO 3 (3 is a prime
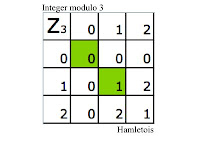
number)
THERE ARE NO ZERO DIVISORS.
As 3 is prime this is a field
1 has an inverse, 2 has an inverse
This field is an integral domain (including addition)
1 is the identity
Notice that 2•2 = 4 and 4 = 1 (mod 3); this is indeed the first time we need of division to find our answer.
So far as before we have that 0 • 0 = 0 and 1 • 1 = 1. Thus as before 0 is a idempotent as well as a nilpotent. The element 1 is only an idempotent. There are no zero divisors.

INTEGER MODULO 4 (4 is a composite number)
THE FIRST ZERO DIVISOR APPEARS, NAMELY: 2.
THIS IS NOT AN INTEGRAL DOMAIN AS IT HAS A ZERO DIVISOR
1 has an inverse, 3 has an inverse
{1,3} form a group of units for Z4
THIS IS NOT A FIELD AS 4 IS NOT PRIME
THIS IS A COMMUTATIVE RING WITH AN IDENTITY =1 (including addition)
Check this one out. This is the first case in which we encounter zero divisors. That is a•b = 0 yet a ≠ 0 nor b ≠ 0 that is 2• 2 = 4 = 0 (mod 4).
0 is a neilpotent, 1 is an idempotent, 0 is also an idempotent. Also this is the first time I distinguish 2 to be both a zero divisor and a nilpotent at the same time.
2 • 2 = 4 = 0 (mod 4)
2 • 3 = 6 = 2 (mod 4)
3 • 2 = 6 = 2 (mod 4)
3 • 3 = 9 = 1 (mod 4)
Notice that : The remainder is the answer of every product when divided by 4.

INTEGER MODULO 5 (5 is a prime number)
NO ZERO DIVISORS.
THIS IS A FIELD AS 5 IS PRIME
THIS IS AN INTEGRAL DOMAIN AS IT DOES NOT HAVE ANY ZERO DIVISORS
1, has an inverse, 4 has an inverse
{1,4} is a group of unit of Z5
1 IS THE IDENTITY FOR THIS FIELD (including the operation of addition of addition)
Notice that there are no zero divisors in the table. The only idempotents are 0 and 1 and the only nilpotent is 0.

INTEGER MODULO 6
THE SECOND SET OF ZERO DIVISORS APPEAR {2,3,4}
MAKING Z6 NOT AN INTEGRAL DOMAIN AS IT HAS ZERO DIVISORS
1 AND 6 ARE THE ONLY ELEMENTS HAVING INVERSES {1,6} FOR A GROUP OF UNITS OF Z6
Def. a is a unit iff ab=1=ba and 1≠0.
THIS IS A COMMUTATIVE RING WITH IDENTITY 1 IF WE CONSIDER BOTH: ADDITION AND SUBTRACTION FOR Z6
Zero divisors appeared in integer modulo 4. Here in integer modulo 6, zero divisors make their appearance again. From the table, 3 and 4 and zero divisors. 0,1,3, and 4 are idempotents. 0 appears to be the only nilpotent. Impotant is the fact that no zero divisor in the modulo is a also a nilpotent element.

INTEGER MODULO 7 (7 IS PRIME)
NO ZERO DIVISORS.
THIS IS A FIELD AND AN INTEGRAL DOMAIN (including addition)
1 is the identity (multiplication)
one is the only element that has inverse
The first thing to notice here is that there is no zero divisors. The only nilpotent is 0. There are two idempotents: 1, and 0.

INTEGER MODULO 8 (8 IS COMPOSITE)
THE THIRD SET OF ZERO DIVISORS APPEAR.
THIS IS NOT AN INTEGRAL DOMAIN AS IT HAS ZERO DIVISORS
NOT A FIELD AS 8 IS NOT PRIME
ONLY A COMMUTATIVE RING WITH IDENTITY 1
1,3,5,7, HAVE INVERSE
{1,3,5,7,} FOR A GROUP OF UNITS OF Z8
Notice that there are 3 zero divisors {2,4,6}. There are also two neilpotents {0,4}. There are also two idempotents {0,1}. Important too is the fact that 4 is both a nilpotent and a zero divisor.

INTEGER MODULO 9 (9 Is a composite number)
THE FOURTH SET OF ZERO DIVISORS APPEAR: {3, 6}. THIS TWO ZERO DIVISORS ARE AMAZINGLY ENOUGH BOTH NILPOTENT ELEMENTS.
NOT AN INTEGRAL DOMAIN AS IT HAS ZERO DIVISORS
As before 0 and 1 are both idempotents. 0 is also, a nilpotent. 3 is also a nilpotent. 6 is also a nilpotent. Notice that 3 and 6 are both zero divisors and nilpotents.

INTEGER MODULO 10 (10 IS NOT PRIME)
THERE ARE ZERO DIVISORS {2,4,5,6,8}. NON OF THIS ZERO DIVISORS IS A NILPOTENT. THE ONLY NILPOTENT IS 0. THE IDEMPOTENT ARE {0,1,5,6}. NOTICE THAT 6 IS BOTH A ZERO DIVISOR AND AN IDEMPOTENT. SO IS 5 ALSO.

INTEGER MODULO 11
THERE ARE NO ZERO DIVISORS
2 IDEMPOTENTS {0,1}
ONE NILPOTENT {0}
NOTICE THAT THE TABLE LOOKS VERY CLEAN.
IDEMPOTENTNILPOTENT






















 INTEGER MODULO 2 ( 2 is a prime number)
INTEGER MODULO 2 ( 2 is a prime number) number)
number)
 INTEGER MODULO 5 (5 is a prime number)
INTEGER MODULO 5 (5 is a prime number) INTEGER MODULO 6
INTEGER MODULO 6 INTEGER MODULO 7 (7 IS PRIME)
INTEGER MODULO 7 (7 IS PRIME) INTEGER MODULO 8 (8 IS COMPOSITE)
INTEGER MODULO 8 (8 IS COMPOSITE)

 INTEGER MODULO 11
INTEGER MODULO 11 https://www3.imsa.edu/programs/e2k/curriculum/68reflections.mod/teaching
https://www3.imsa.edu/programs/e2k/curriculum/68reflections.mod/teaching
